ความโน้มถ่วง
ในทางฟิสิกส์ ความโน้มถ่วง หรือ แรงโน้มถ่วงมวล แรงโน้มถ่วงเป็นหนึ่งในสี่แรงหลัก ซึ่งประกอบด้วย แรง โน้มถ่วงแรงแม่เหล็กไฟฟ้า แรงนิวเคลียร์แบบอ่อน และ แรงนิวเคลียร์แบบเข้ม ในจำนวนแรงทั้งสี่แรงหลัก แรงโน้มถ่วงมีค่าน้อยที่สุด ถึงแม้ว่าแรงโน้มถ่วงจะเป็นแรงที่เราไม่สามารถรับรู้ได้มากนักเพราะความเบา บางของแรงที่กระทำต่อเรา แต่ก็เป็นแรงเดียวที่ยึดเหนี่ยวเราไว้กับพื้นโลก แรงโน้มถ่วงมีความแรงแปรผันตรงกับมวล ไม่มีการลดทอนหรือถูกดูดซับเนื่องจากมวลใด ๆ ทำให้แรงโน้มถ่วงเป็นแรงที่สำคัญมากในการยึดเหนี่ยวเอกภพไว้ด้วยกัน
นอกเหนือจากความโน้มถ่วงที่เกิดระหว่างมวลแล้ว ความโน้มถ่วงยังสามารถเกิดขึ้นได้จากการที่เราเปลี่ยนสภาพการเคลื่อนที่ตาม กฏการเคลื่อนที่ของนิวตัน เช่น การเพิ่มหรือลดความเร็วของวัตถุ การเปลี่ยนทิศทางการเคลื่อนที่ เป็นต้น
กฎ ความโน้มถ่วงของนิวตัน
ในปี
พ.ศ. 2230 ไอแซก นิวตัน ได้ค้นพบกฎความโน้มถ่วงดังนี้
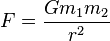
เมื่อ:
- F เป็นความโน้มถ่วงระหว่างมวลทั้งสอง
- G เป็นค่าคงที่ความโน้มถ่วง
- m1 เป็นมวลของวัตถุแรก
- m2 เป็นมวลของวัตถุที่สอง
- r เป็นระยะห่างระหว่างวัตถุทั้งสอง
นั่นคือความโน้มถ่วงแปรผันตรงกับมวล (มวลมากก็มีความโน้มถ่วงมาก) และแปรผกผันกับระยะห่างกำลังสอง (ระยะห่างมากก็มีความโน้มถ่วงน้อย)
ทฤษฎี สัมพัทธภาพทั่วไป
อัลเบิร์ต ไอน์สไตน์ ได้เผยแพร่
ทฤษฎีสัมพัทธภาพทั่วไปในปี
พ.ศ. 2459โดยเนื้อหาแสดงถึงการอธิบายความโน้มถ่วงที่ มีพื้นฐานมาจาก
ทฤษฎีสัมพัทธภาพพิเศษและ
กฎความโน้ม ถ่วงของนิวตันในรูปแบบของ
กาลอวกาศ (Spacetime) เชิงเรขาคณิตที่สามารถอธิบายได้ด้วย
สมการสนามของไอ น์สไตน์(Einstein field Equation)ดังนี้
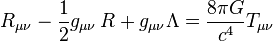
- เมื่อ Rμν เป็น ริชชี่เทนเซอร์ความโค้ง (Ricci Tensor Curvature)
- R เป็น ความโค้งเชิงสเกลาร์ (Scalar Curvature)
- gμν เป็น เมตริกซ์เทนเซอร์
 เป็น ค่าคงตัวจักรวาล (Cosmological Constant)
เป็น ค่าคงตัวจักรวาล (Cosmological Constant)- G เป็น ค่านิจโน้มถ่วงสากล (Gravity Constant)
- c เป็น ความเร็วแสง
- Tμν เป็น เทนเซอร์ความเค้น-พลังงาน (Stress-Energy Tensor)
 เป็น ค่าคงตัวจักรวาล (Cosmological Constant)
เป็น ค่าคงตัวจักรวาล (Cosmological Constant)
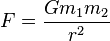
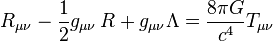
ไม่มีความคิดเห็น:
แสดงความคิดเห็น